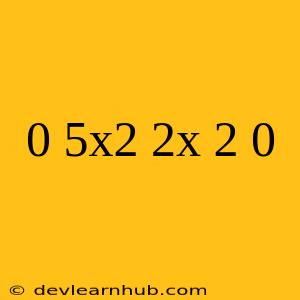Tentu, ini artikel tentang persamaan kuadrat $0.5x^2 - 2x + 2 = 0$:
Solving the Quadratic Equation: 0.5x^2 - 2x + 2 = 0
This equation is a quadratic equation in the standard form: ax^2 + bx + c = 0, where a = 0.5, b = -2, and c = 2.
Here are the common methods to solve quadratic equations:
1. Factoring
- Identify factors: In this case, the equation cannot be easily factored into two binomials with integer coefficients.
2. Completing the Square
- Isolate the x^2 and x terms: 0.5x^2 - 2x = -2
- Divide both sides by the coefficient of x^2 (0.5): x^2 - 4x = -4
- Complete the square on the left side: Take half of the coefficient of the x term (-4), square it (4), and add it to both sides. x^2 - 4x + 4 = -4 + 4
- Factor the left side as a perfect square trinomial: (x - 2)^2 = 0
- Solve for x: x - 2 = 0 x = 2
Therefore, the solution to the equation is x = 2.
3. Quadratic Formula
- Apply the formula: The quadratic formula provides a direct solution for any quadratic equation. x = (-b ± √(b^2 - 4ac)) / 2a
- Substitute the values: x = (2 ± √((-2)^2 - 4 * 0.5 * 2)) / (2 * 0.5) x = (2 ± √(4 - 4)) / 1 x = (2 ± √0) / 1 x = 2
Therefore, the solution to the equation is x = 2.
Conclusion
Using different methods, we find that the equation 0.5x^2 - 2x + 2 = 0 has a single solution, x = 2. This means the parabola represented by the equation intersects the x-axis at only one point.